Powerball is a lottery game available for play in 44 states in the United States and in the District of Columbia, Puerto Rico and the US Virgin Islands. It is a “mega” lottery because of the usually huge jackpot. As of the writing of this post, the estimated jackpot is $113 million (see the below picture). The largest Powerball jackpot is $1.59 billion on January 13, 2016 (this was also the largest in US lottery history). The average Powerball jackpot is $62.71 million. Recent jackpots had been in the range of hundreds of million dollars.
With such large jackpots, it is not surprising that Powerball is a popular lottery game, especially when the impending jackpot is in the hundreds of millions dollars. Bear in mind that the odds of winning the jackpot are slim: 1 in 292,201,338, i.e. one in over 292 million. This post is to demonstrate how to mathematically derive the winning odds of the jackpot and other smaller prizes of Powerball (the first objective). Calculating the odds is a great math lesson. It is equally interesting and equally important to make sense of the large numbers in the small winning odds. The second objective is to focus on the dim prospect of Powerball players as told by the mathematical odds.
Figure 1 – Powerball Results on April 26, 2017

___________________________________________________________________________
The Game of Powerball
This is how the game is played. In a Powerball playslip, a player picks 5 numbers from 1 through 69 and 1 number from 1 through 26 (this is the Powerball number). Drawings are held Wednesday and Saturday evenings at 10:59 p.m. Eastern Time. In each drawing, five balls are drawn from a drum with 69 white balls (labeled 1 through 69) and one ball is drawn from a drum with 26 red balls (labeled 1 through 26). Figure 1 above shows that the winning numbers on April 26, 2017 are 1, 15, 18, 26 and 51 (white) and 26 (red). The winnings are determined by whether the numbers in the playslip match the balls drawn at the Powerball drawing.
The grand prize is awarded to the player (or players) whose ticket matches all of the numbers on the five chosen white balls and the one chosen red ball. Smaller prizes are awarded to players whose tickets match fewer number of white balls with or without the red ball. The following table shows the levels of prizes and the odds. These Powerball payout rules had been in place since October 7, 2015.
Figure 2 – Powerball Prizes and Odds

As shown by the table, the prizes are for scenarios ranging from matching zero white balls to all 5 of the white balls (with or without the match of the red ball). Of course, matching all 6 balls would lead to the grand prize. Matching just the 5 white balls without the red ball would be the fixed prize of $1 million. Matching any 4 of the white balls plus the red ball would lead to the prize of $50,000. The rest of the prizes are for practically insignificant amounts.
Each Powerball ticket is $2. For an additional $1 per game, a player may activate the Power Play option. When this option is activated, the lower prizes that are $50,000 or less are multiplied by a factor from 1 up to 5 or 10 (10x is available when the jackpot is under $150 million). With the Power Play Option, the prize for the “5 white balls and no red ball” match is increased to $2 million. That is, the “5 + 0” prize is doubled under the Power Play Option. For further information on Powerball, see the Wikipedia entry.
The odds represented in the above table are essentially winning probabilities for a Powerball player (per $2 bet). The odds for the grand prize is 1 in 292,201,338. So the probability of winning the grand prize with one ticket is 1 / 292,201,338, which of course is essentially zero. This probability is essentially this statement: out of 292,201,338 different possible Powerball combinations and only one of them is the winning combination.
The odds for the $1 million prize is 1 in 11,688,353.52, about 1 in 11 million (still very slim odds). So the probability of winning $1 million with one ticket is 1 / 11,688,353.52, which is also essentially zero. Note that 1 / 11,688,353.52 is the same as 25 / 292,201,338. This last probability is the statement: out of 292,201,338 different possible Powerball combinations, only 25 of them are winning (i.e. matching all 5 white balls without the matching the red Powerball number).
Thus calculating the odds for Powerball (or any other lottery game for that matter) is about counting correctly the number of possible lottery ticket combinations (the denominator) and counting the number of winning tickets (the numerator). So this is a counting exercise. In the area of mathematics called combinatorics, which at the elementary level concerns with the counting of number of ways objects can be chosen from a set (a set of balls in the case of lottery). Several previous posts of this blog are devoted to this subject. We will reference them when necessary. However, we strive to make the discussion here as self contained as possible.
___________________________________________________________________________
Using a Toy Lottery
As indicated above, there are 292,201,338 different possible Powerball tickets. Out of these, there are 25 possible winning pickets for the $1 million prize. Of the 292,201,338 possible tickets, there are 320 possible winning tickets for the $50,000 prize. Instead of attacking these problems head on, we use a “toy” lottery to illustrate the idea. Any reader who feels that such introduction is not needed can skip to the next section.
Based on the last paragraph in the preceding section, the winning probability is the number of possible ways to win over the number of possible “tickets.”
Probability of winning = 
For example, if 40 tickets are sold in a raffle and only one of them is the winner, then the odds of winning would be 1 in 40. The probability of winning would be 1 / 40 = 0.025 (2.5% chance). If two of the 40 tickets are winners, then the odds are 1 in 20. The probability of winning would then be 2 / 40 = 0.05 (5% chance). Though the Powerball calculation is based on this simple idea, there are subtle points that need to be addressed in order to fully understand the calculation. So we take the approach of using a toy lottery.
Let’s call the game “toy Powerball.” The player picks two numbers from 5 white balls (labeled 1 through 5) and picks one number from 4 red balls (labeled 1 through 4). The prizes are:
- grand prize (match all 2 white balls and 1 red ball),
- $100 prize (match 2 white balls and not matching the red ball),
- $10 prize (match 1 white ball and the red ball).
How many different possible tickets are there? Since there are two drawings (one for the white ball and one for the red ball), we need to count them separately and multiply the results. Since there are only 5 white balls, we can actually count the number of ways to choose 2 balls out of 5 white balls.
1, 2
1, 3
1, 4
1, 5
2, 3
2, 4
2, 5
3, 4
3, 5
4, 5
There are obviously 4 ways to choose one ball out of 4 red balls. So the total number of different possible tickets are 10 x 4 = 40. This is based on the so called multiplication principle – if one event can occur in  ways and another event can occur, independent of the first event, in
ways and another event can occur, independent of the first event, in  ways, then the two events together can occur in
ways, then the two events together can occur in 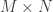 ways. The multiplication principle, discussed here, will be a great help in calculating the odds. For example, the first event is the choosing of the white balls and the second event is the choosing of the red balls. This idea can be used to find the number of possibilities in both the denominator and the numerator.
ways. The multiplication principle, discussed here, will be a great help in calculating the odds. For example, the first event is the choosing of the white balls and the second event is the choosing of the red balls. This idea can be used to find the number of possibilities in both the denominator and the numerator.
There is only one possible winning ticket for the grand prize (of course, if two people pick the same winning combination, they will split the prize). So the odds for winning the grand prize is 1 in 40. The probability of winning the grand prize is 1 / 40 = 0.025 (2.5%).
Is there a way to calculate the number of ways to choose two balls out of 5 white balls (labeled 1 through 5) without writing down all possibilities? This will be key to the Powerball calculation. There are two ways. One is an intuitive approach using the multiplication principle and the other is to use a formula for combination.
The first idea. Choosing two numbers is like filling two spots with numbers. In this case, the first spot has 5 choices and the second spot has 4 choices after the first spot is filled. This gives a total of 5 x 4 = 20. But 20 is an over count. For example, the result 3-2 (first number is 3 and the second number is 2) is actually the same as 2-3 as far as the lottery is concerned. So each 2-number combination appears twice in the count of 20. Thus dividing by 2 gives 20 / 2 = 10.
The other way is via a formula for combination. In the toy Powerball example, we need to choose 2 balls out of 5 balls. The following is the calculation.
Let’s unpack this calculation. The notation 5!, read 5 factorial, is 5 x 4 x 3 x 2 x 1 = 120, in other words, obtained by multiplying together 5 and all the positive integers below 5. Thus 6! = 6 x 5 x 4 x 3 x 2 x 1 = 6 x 120 = 720. In general, whenever  is a positive integer,
is a positive integer, 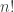 , read
, read  factorial, is obtained by multiplying
factorial, is obtained by multiplying  and all the positive integers below
and all the positive integers below  . To make the calculation works out, we define 0! = 1.
. To make the calculation works out, we define 0! = 1.
Is there any natural interpretation of factorial? For example, 5! is the number ways to arrange 5 people in a row for a group photo. Five people are to be assigned into 5 spots. There are 5 possibilities for the first spot, 4 possibilities for the second spot after the first person is chosen and so on. By the multiplication principle, the total number of ways to do this would be 5 x 4 x 3 x 2 x 1. In general 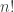 is the number of ordered arrangements of
is the number of ordered arrangements of  objects.
objects.
Thus the number of ways to choose 2 balls out of 5 balls is 10 (also the number of ways to choose two people out of 5 to form a committee of 2, the number of ways to choose 2 students out of 5 for awards, or the number of ways to choose 2 ice cream flavors out of 5 – the possibility is endless). The notation for “choose 2 from 5” is 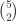 . The top number in this notation is the total number of objects to choose from and the bottom number is the number of objects to be chosen. In general, the number of ways to choose
. The top number in this notation is the total number of objects to choose from and the bottom number is the number of objects to be chosen. In general, the number of ways to choose  objects out of
objects out of  objects is
objects is

The number 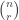 is called the number of possible combinations of
is called the number of possible combinations of  objects chosen
objects chosen  at a time. Other notations include
at a time. Other notations include 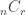 and
and 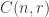 . Regardless the notations, it is the number of ways to choose
. Regardless the notations, it is the number of ways to choose  objects from a set of
objects from a set of  objects or the number of different groups of size
objects or the number of different groups of size  that can be chosen from a set of
that can be chosen from a set of  distinct objects. Many calculators have a function for the number
distinct objects. Many calculators have a function for the number 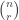 (in a calculator the notation is probably
(in a calculator the notation is probably 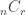 ). If it is to be calculated by hand, bear in mind that
). If it is to be calculated by hand, bear in mind that 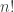 , factorial of the total number of object, is in the numerator and the two factorials in the denominator are
, factorial of the total number of object, is in the numerator and the two factorials in the denominator are  and
and 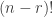 where
where  is the number of objects to be chosen. Note that the sum of
is the number of objects to be chosen. Note that the sum of  and
and 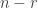 is
is  .
.
For more information about how to calculate combination, see here and the summary section here.
Let’s look at the second prize in toy Powerball – match 2 white balls and no match for red ball. As example, let’s say the winning numbers are 1 and 3 (white) and 2 (red). How many 3-number combinations satisfy the winning criteria for this prize – matching two white numbers and not the red number? There is still only one way to match the two white numbers. But there are 3 ways to not match the red winning numbers (the non-winning red numbers would be 1, 3, and 4). The number of possible winning tickets would be 1 x 3 = 3. So the odds for winning the $100 prize are 3 in 40. The probability of winning the $100 prize is 3 / 40 = 0.075 (7.5%).
The third prize is $10 won by matching 1 white ball and 1 red ball. Again, using the example of winning numbers of 1 and 3 (white) and 2 (red), how many 3-number combinations satisfy the winning criteria for this prize – matching 1 white number and the red number? Remember that the player of the game chooses 2 white numbers and 1 red number. Since there is only 1 correct match for white number, there are 1 winning white number and 1 non-winning white number in the ticket. There are two ways to match 1 winning white number (1 or 3) and there are 3 ways to match 1 non-winning white number (2, 4 and 5). Of course, there is only one way to match the winning red number. The number of possible winning tickets would be 2 x 3 x 1 = 6 (by the multiplication principle again). This observation will be crucial in understanding the Powerball calculation below.
So the odds for winning the $10 prize are 6 in 40. The probability of winning would be 6 / 40 = 0.15 (15%).
___________________________________________________________________________
Back to Powerball
The winning probability of a prize in a lottery would be the fraction of all of the possible lottery numbers which count as winning. In other words, the winning probability would be a fraction with the denominator being the total number of possible number combinations that can be picked by the lottery players and the numerator being the number of possible winning combinations. So the denominator is always fixed for a given lottery. The numerator would vary depending on the prize. The bigger the prize, the smaller the numerator (the harder it is to win).
For the Powerball game uses a 6-number combination (5 white numbers + 1 red number). the 5 white numbers are chosen out of 69 numbers and the 1 red number is chosen out of 26 numbers. So based on the discussion in the preceding section, the total number of possible 6-number combinations would be:
Total Number of Possible Powerball Combinations
There are  many possible 5-number sets that can be picked from 69 numbers. There are over 11 millions ways to match the 5 winning white balls. There are
many possible 5-number sets that can be picked from 69 numbers. There are over 11 millions ways to match the 5 winning white balls. There are 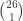 = 26 possible ways to pick one number from 26 numbers. By the multiplication principle, the product of these numbers would be the total number of possible Powerball combinations.
= 26 possible ways to pick one number from 26 numbers. By the multiplication principle, the product of these numbers would be the total number of possible Powerball combinations.
For the winning probability of any Powerball prize, the denominator would be 292,201,338, which is a staggering number. To help with understanding what should go into the numerator, let’s use the latest winning combination: 1, 15, 18, 26 and 51 (white balls) and 26 (red ball), drawn on April 26, 2017 (shown in Figure 1 above). So all the winning calculations below are based on this example. The number that goes into the numerator would be the number of tickets matching some or all of the white numbers with or without matching the red number depending on the rules. Let’s consider the prizes one by one.
Match 5 white balls + 1 red ball (grand prize)
There is only winning combination. So the winning probability is 1 over 292,201,338. The winning odds would be 1 in 292,201,338.
Match 5 white balls + no red ball ($1,000,000)
Probability of winning = 
The relevant question here is: how many ticket combinations are that that match all 5 winning white numbers and that do match the 1 red winning number? There is only one way to match all 5 white numbers 1, 15, 18, 26 and 51 (as in the grand prize). There are 25 ways to not match the winning red number 26 (1 through 25). So the numerator is 25. So the odds for winning $1 million are 25 in 292,201,338 or 1 in 11,688,053.52 (1 in over 11 million).
Match 4 white balls + 1 red ball ($50,000)
Probability of winning = 
To win, a player needs to match 4 of the white numbers. To count all the winning combinations, choose 4 numbers from the 5 winning white numbers and choose 1 number from the 64 non-winning white numbers Recall that the ticket has 5 white numbers. If only 4 of them match the winning numbers, then one of the white numbers on the ticket must from a non-winning white number.
Furthermore, choose 1 number from the 1 winning red number and 0 numbers from the 25 non-winning red numbers. This observation explains what appear in the numerator. Then the odds for winning the $50,000 prize are 320 in 292,201,338 or 1 in 913,129.18.
Match 4 white balls + no red ball ($100)
Probability of winning = 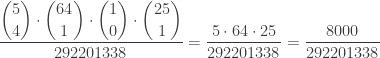
Without the red ball match, there are more ways to win (25 more to be precise). To count the number of winning tickets, choose 4 from the 5 winning white numbers, choose 1 from the 64 non-winning white numbers, choose 0 from the 1 winning red number and choose 1 from the 25 non-winning red numbers. Doing this gives 8,000. Then the odds for winning the $100 prize are 8,000 in 292,201,338 or 1 in 36,525.17.
Match 3 white balls + 1 red ball ($100)
Probability of winning = 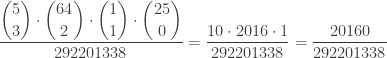
To count the number of winning tickets, choose 3 from the 5 winning white numbers, choose 2 from the 64 non-winning white numbers, choose 1 from the 1 winning red number and choose 0 from the 25 non-winning red numbers. Doing this gives 20,160. Then the odds for winning the second $100 prize are 20,160 in 292,201,338 or 1 in 14,494.11.
Match 3 white balls + no red ball ($7)
Probability of winning = 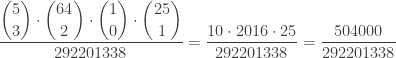
Let’s use the latest winning numbers 1, 15, 18, 26 and 51 (white balls) and 26 (red ball) to illustrate. How many ticket combinations would satisfy this criteria: match 3 numbers from 1, 15, 18, 26 and 51 (white balls) and not match the winning red number 25? The answer is the number of ways to choose 3 from 1, 15, 18, 26 and 51, choose 2 from the other 64 white numbers, choose 0 from 1 winning red number (26) and choose 1 from 25 non-winning red numbers. This explains what is in the numerator, which is 504,000. Then the odds for winning the first $7 prize are 504,000 in 292,201,338 or 1 in 579.76.
Match 2 white balls + 1 red ball ($7)
Probability of winning = 
Using similar idea to set up the numerator, the numerator is 416,640. Then the odds for winning the second $7 prize are 416,640 in 292,201,338 or 1 in 701.33.
Match 1 white ball + 1 red ball ($4)
Probability of winning = 
As discussed earlier, when the match of the white balls is partial, the white numbers that do not match the winning white numbers must come from the 64 non-winning numbers. So we choose 1 from 5 winning white numbers and choose 4 from 64 non-winning white numbers. There is only one way to pick the winning red number. The numerator is 3,176,880. Then the odds for winning the first $4 prize are 3,176,880 in 292,201,338 or 1 in 91.98.
Match no white ball + 1 red ball ($4)
Probability of winning = 
The numerator is 7,624,512. Then the odds for winning the second $4 prize are 7,624,512 in 292,201,338 or 1 in 38.32.
The overall odds of winning a prize
The total number of possible 6-number combinations that result in a prize is obtained by summing all the numerators in the above calculation of odds. There is a total of 11,750,538 many possible prizes. The following table shows the breakdown.
Number of Possible Prizes
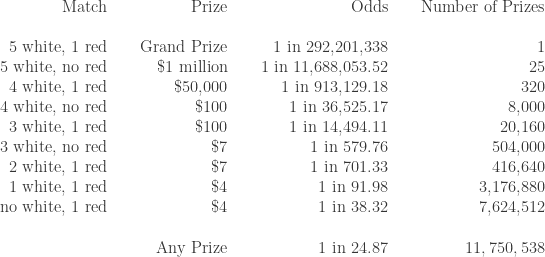
The odds of winning any prize would be 11,750,538 in 292,201,338, or 1 in 24.87. It ought to be mentioned that the last column in the table is only for the number of potential prizes in a category (they are number of possible winning combinations). A prize is awarded only when someone purchased the winning combination. For example, on April 26, 2017, no one won the grand prize since no one had purchased the winning numbers of 1, 15, 18, 26, and 51 and 26. No one had won the $2 million prize for match 5 power play. However, there were three winners for the match 5 (they did not pay for the extra power play option). There are 25 possible winning combinations but only three were won. Figure 1 also shows that there were 592,253 winners on that day. Potentially, there could be 11,750,538 (or more) winners in each drawing.
Remarks on Calculations
First, we emphasize again the point that has been made several times already. The smaller prizes only require partial matching of white numbers with or without matching of the red number. The matching of white numbers must account for winning and non-winning numbers. For example, if the prize requires the matching of 3 white numbers, then we need to count 3 numbers from the 5 winning white numbers and 2 numbers from 64 non-winning white numbers. Hence  . Recall that to play Powerball, the player chooses 5 numbers from the 69 white balls. If the player matches only 3 winning white balls, the other two white numbers chosen by the player must come from the 64 non-winning white balls.
. Recall that to play Powerball, the player chooses 5 numbers from the 69 white balls. If the player matches only 3 winning white balls, the other two white numbers chosen by the player must come from the 64 non-winning white balls.
The odds for the last prize (matching the red number only) are not 1 in 26. This is a common misconception. There are only 26 red balls. So matching the red ball must have a 1 in 26 chance. However, we cannot ignore the white balls! The fact that only the red ball is matching means that the 5 white numbers chosen by the player must come from the 64 non-winning white numbers. So the correct value to go into the numerator is  .
.
___________________________________________________________________________
Do You Feel Lucky Today?
The odds for winning the Powerball jackpot are mathematically zero (being 1 in 292 millions). The entire population of the United States is 321.4 millions in 2015, with 248 millions of them age 18 or over. If every adult in the U.S. purchases a Powerball ticket, it is still possible that there will be no winner of the grand prize (but there could be a few $1 million winners). To get a sense of how big the number 292 million is, look at this piece from WSJ. The piece strives to illustrate how vast a quantity 292,201,338 is. Just to scroll the page over that many dots is a near impossible task.
One thing is for sure. With no winners of jackpot in a several drawings in a row, the excitement for Powerball is turned into a frenzy. In fact, the last revision of the Powerball rules in 2015 made winning of the jackpot much less likely. As a result the jackpot usually keeps building until it reaches hundreds of millions range or the 1 billion range. The rules were designed to rachet up the excitement and as a result driving up sales (discussed in this piece from Washington Post).
Playing Powerball is an excellent entertainment. With a $2 admission price, you can dream and fantasize for a few days. Once a week habit would be about $100 a year in entertainment cost. Regular customers of Starbucks would spend more than that amount. Of the regular lottery players, roughly the top 5% spend a few thousand dollars a year (a hundred thousand dollars on average in their lifetime, assuming no interest) for an illusive chance to win $1 million or more. What if these regular players invest the money elsewhere?
If they invest the money instead on a conservative fund earning 2% a year, they would accumulate an nest egg of hundreds of thousands of dollars. Assuming a rate of returns at 2% a year, investing $3,000 a year would yield approximately $185,000. In fact, if they invest in a broad base stock market index (e.g. S&P 500 index), they would do even better in the long run. The long run historical S&P 500 returns are around 10% a year (7% after inflation). Assuming a rate of returns at 7% a year, investing $3,000 a year would yield around $640,000!
Even in the rare chance that someone wins $1 million, the winning is taxed and would be greatly reduced, e.g. the winning could be $500,000 after tax. Thus the rates of return of a lifetime investment in playing lottery are not as great as people imagine. Without winning, the lifetime lottery investment of a few thousands dollars a year would be money going down the drain. For a more detailed discussion, see this piece from Washington Post.
The calculation of the Powerball winning odds is a great math lesson. Rather than looking at the winning odds, perhaps it is more instructive to look at losing odds. The odds for not winning the Powerball grand prize (per $2 bet) are 292,201,337 to 292,201,338, which are essentially 1 in 1.
___________________________________________________________________________
 2017 – Dan Ma
2017 – Dan Ma
-disk game requires a minimum of
moves. Thus the tower of Hanoi is a concrete example of an illustration of exponential growth – increasing the size of the game by one disk doubles the time required to play the game.
disks, move the top
disks into the intermediate rod (by following the rules of course). Then move the largest disk in the starting rod into the destination rod. To finish off the game, move the
disks in the intermediate rod into the destination rod. So the
-disk game is executed by playing two
-disk games with the move of the largest disk in between. So the tower of Hanoi is a great introduction to a recursive algorithm. The tower of Hanoi game would be a great computer programming exercise.

moves, which is 4,294,967,295. Assuming one second per move, this would be over 136 years! If the workers in the museum is required to move the disks from one rod to another rod by following the rules of the game, that’s would be job security!
, which is 18,446,744,073,709,551,615, when converted to years would be 585 billion years (again, assuming one second per disk). In contrast, the age of the universe is believed to be 13.82 billion years. The age of the sun is believed to be 4.6 billion years. The remaining lifetime of the sun is believed to be around 5 billion years. So by the time the sun dies out the game is still not finished!
2017 – 2023 – Dan Ma